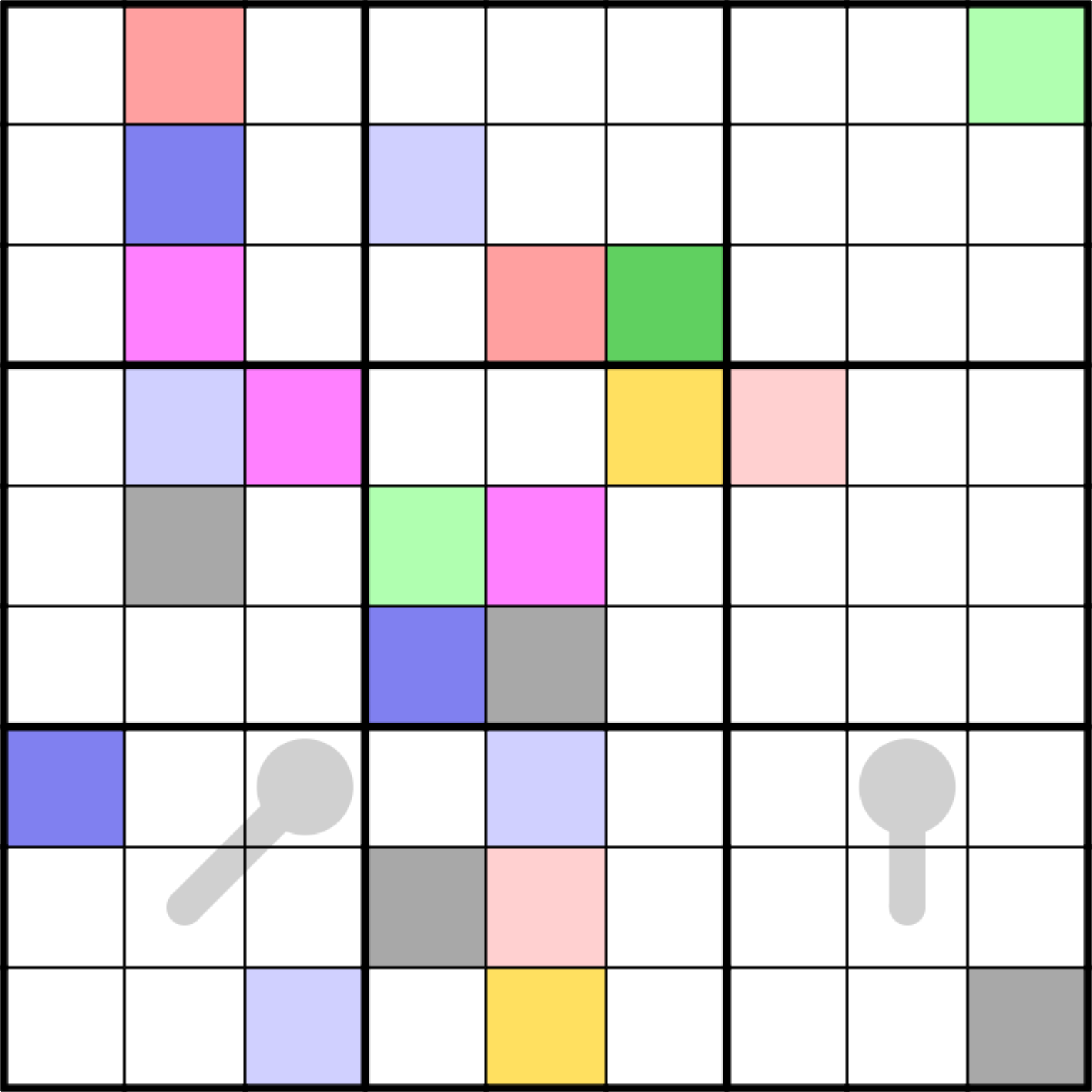
After receiving feedback on Thinking in Color 1, I decided to remove the anti-king constraint to make the solve path more interesting. I liked the finish of the first puzzle, so I kept it. Because of the specific constraints of this puzzle, I learned how to use the Z3 constraint solver, which I used to find a valid grid.

The rules are as follows:

Normal sudoku rules apply (the digits 1-9 must appear exactly once in each row, column, and box). Orthogonally adjacent digits cannot be consecutive. For the purposes of this puzzle, the digits 1 and 9 are considered consecutive. Digits a knight’s move (in chess) away cannot be the same. Along thermometers (gray lines), digits must increase from the bulb to the tip. Cells that are colored the same contain the same digit.